Ligeti's Combinatorial Tonality
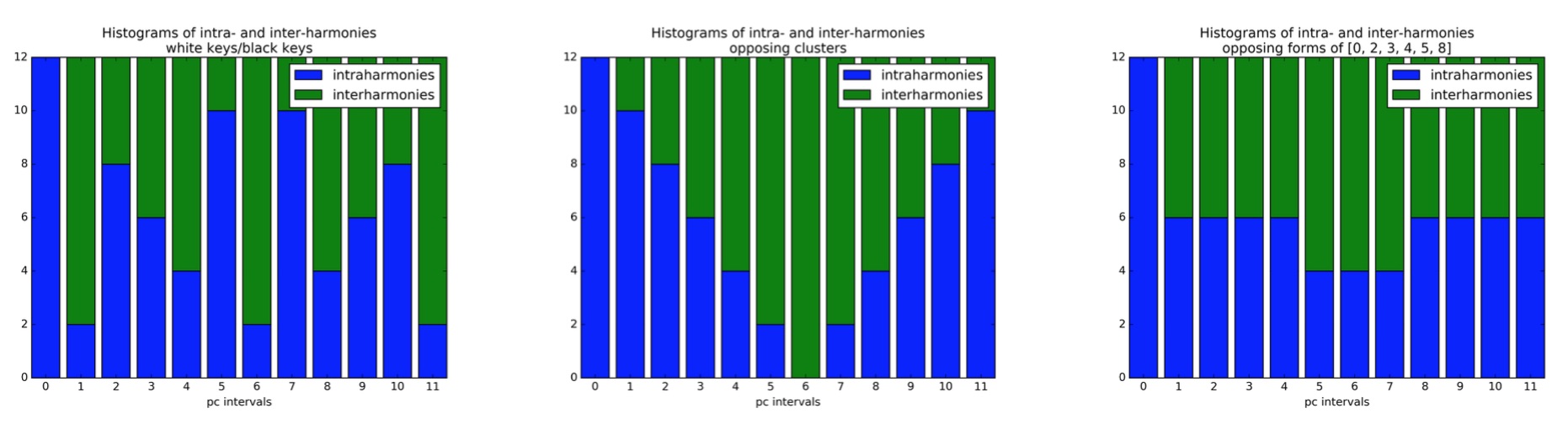
Recent work on Ligeti’s use of complementary collections in his late works, which Richard Steinitz refers to as “Combinatorial Tonality,” presented at the 2017 Conference on Mathematics and Computation in Music. (An earlier version presented at the 2017 Joint Mathematics Meeting of the American Mathematical Society and Mathematical Association of America.) These works exploit the intervallic content both within and between collections. The intra- and inter-harmonic potentials are analytically useful and exhibit nice mathematical properties. Analysis of Ligeti’s Désordre develops ideas in Lawrence Quinnett’s FSU doctoral treatise Harmony and Counterpoint in Ligeti Études.
Infinite Canons

Infinite Canons is an ongoing series of canons with infinite solutions. More specifically, each canon is based on a melodic line that can be combined in any number of voices, in any tempo ratios (rational or irrational), and with each voice moving either forward or backward through the line, while maintain harmonic consistency. You can read an in-depth description or listen to Canonic Offerings, an original composition based on a limited set of these combinations.
Performing the Irrational

While many of Conlon Nancarrow’s Studies for Player Piano have been arranged for live human performance, the Studies that are based on irrational tempo ratios pose extreme rhythmic challenges that would seem impossible to overcome without mechanical assistance. Nonetheless, Paul Usher’s arrangement of Study 33, Canon 2:√2, has been successfully performed and recorded by the Arditti Quartet. The purpose of this paper is to explore some of the compositional, mathematical, and performance issues involved in the approximation of irrational rhythms, concentrating on Usher’s arrangement of Study 33 in order to more fully understand and appreciate this remarkable feat.
Performing the Irrational Paul Usher’s Arrangement of Nancarrow’s Study No. 33, Canon 2:√2, Music Theory Online, 20.1, 2014.
Sturmian Canons
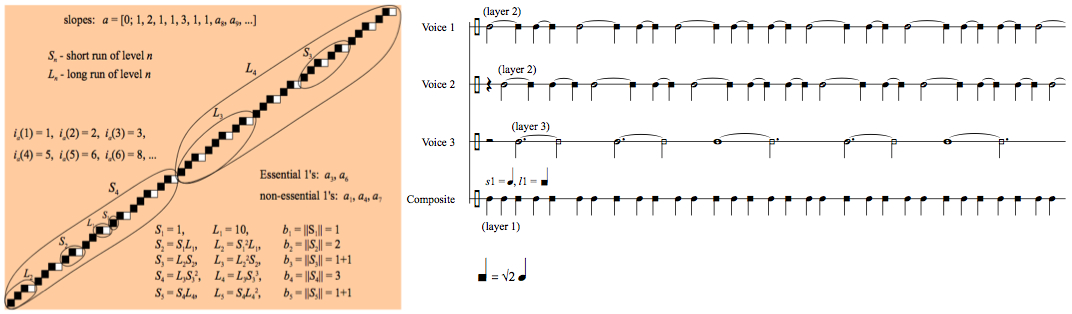
Investigation into the structural properties of rhythmic canons based on Sturmian words. These Sturmian canons are aperiodic, hierarchical, and potentially self-similar rhythmic patterns that give rise to aperiodic (thus infinite) rhythmic canons, tilings, and polyrhythms. (Left-side of the above image is taken from Hanna Uscka-Wehlou’s work on digital lines of irrational slope, which has a natural interpretation in terms of rhythmic canons. My own work teases out these implications and extends her results to hierarchical periodicities manifest in terms of canonic structure.)
Sturmian Canons, In J. Yust, J. Wild, and A. Burgoyne (eds.): Mathematics and Computation in Music: Fourth International Conference, MCM 2013.
Representations of Tempo
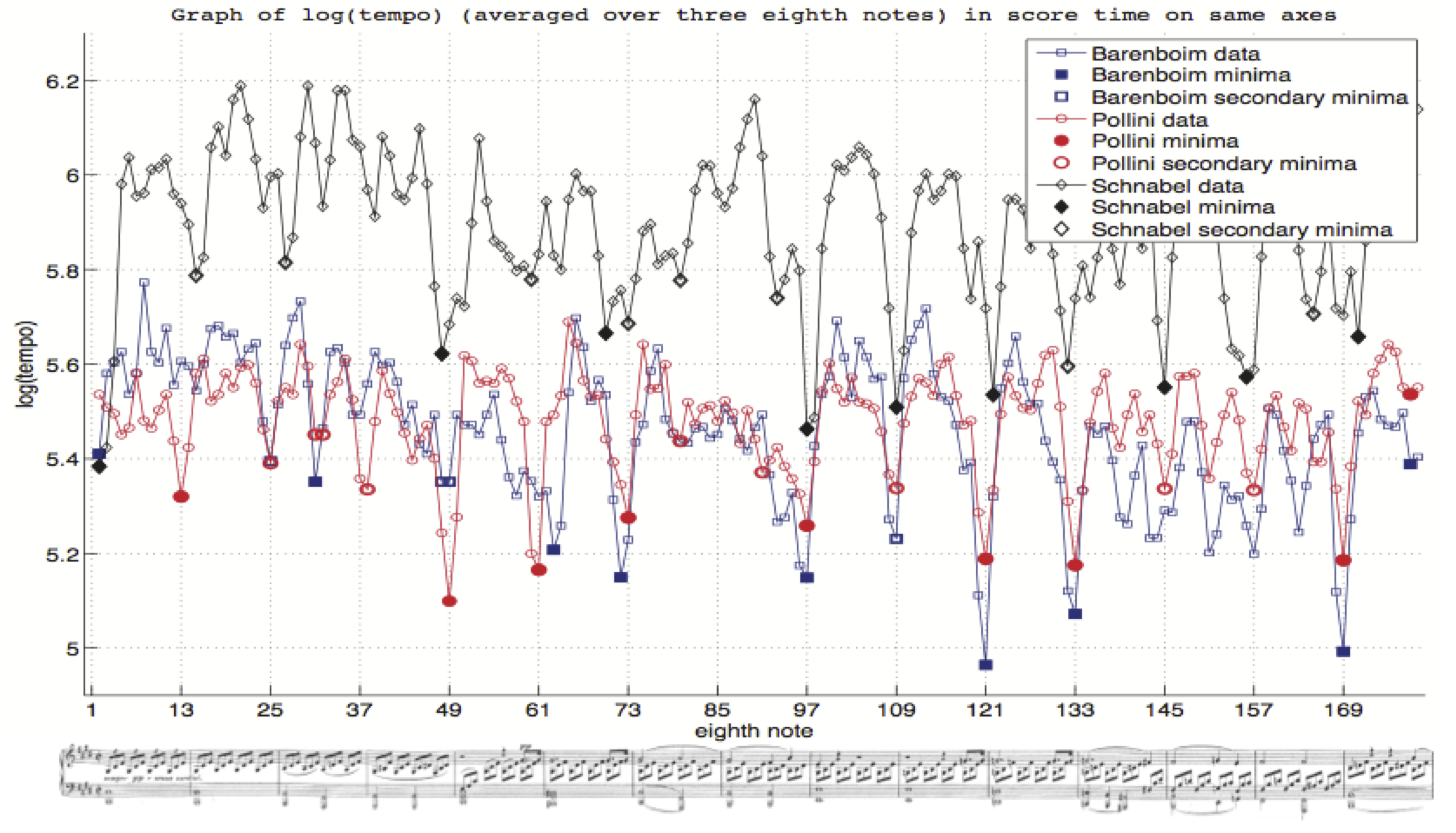
Tempo is an important parameter that is varied and analysed in music performance. We argue that it is important to consider both tempo and log(tempo) in score time as well as performance time in the analysis of performances; performance time mirrors listeners’ real time experience, and log(tempo) gauges proportional tempo changes. As demonstration, we revisit Chew’s (2012) score time tempo analysis of performances of Beethoven’s “Moonlight” Sonata, and generate new results using log(tempo) and performance time. We show that extreme differences in score time tempo are ameliorated by considering log(tempo) and performance time, that the performers employed similar log(tempo) ranges and phrase lengths (in performance time), and that long score time phrases do not necessarily map to lengthy performance time spans due to speedier phrase traversal times. The results suggest that log(tempo) range and maximum performance time phrase length may act as perceptual constraints on the shaping of a performance.
Chew, E. and C. Callender (2013). Conceptual and Experiential Representations of Tempo: Effects on Expressive Performance Comparisons. In J. Yust, J. Wild, and A. Burgoyne (eds.): Mathematics and Computation in Music: Fourth International Conference, MCM 2013.
Continuous Harmonic Spaces
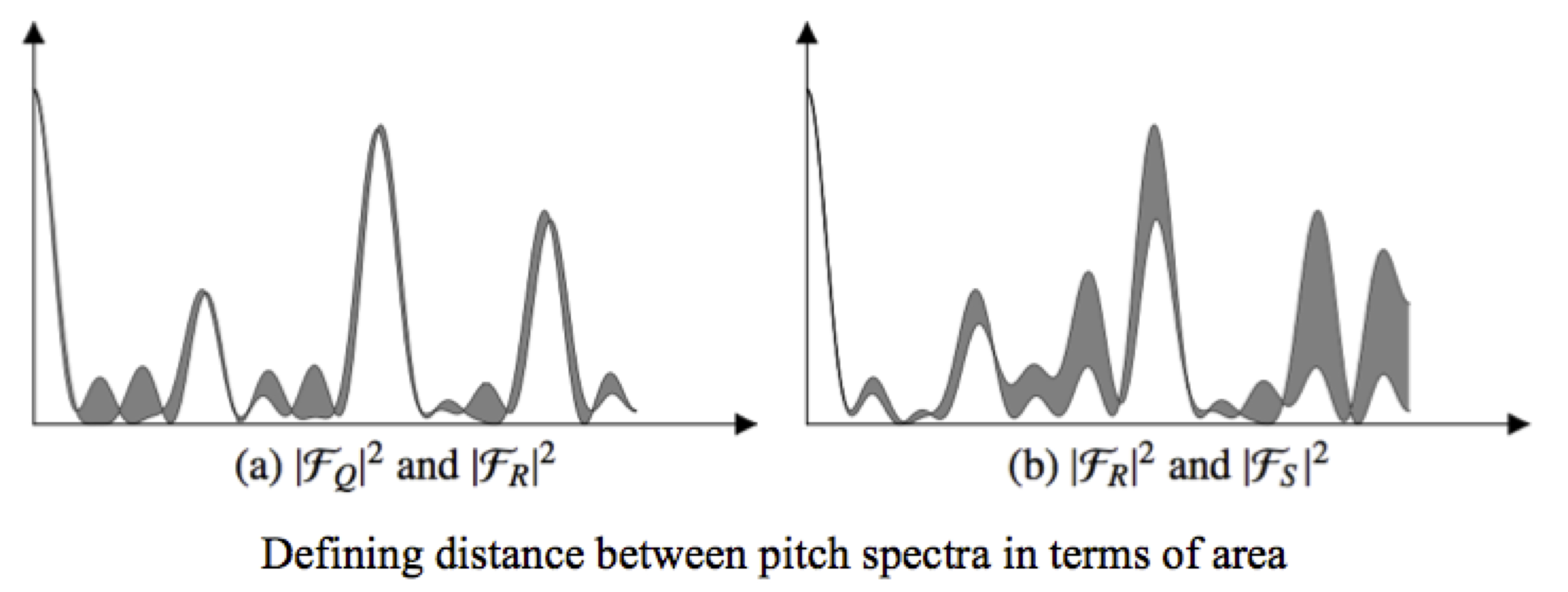
Recent work by Ian Quinn investigates the harmonic quality of pitch-class sets through the use of the discrete Fourier transform. This paper uses the continuous Fourier transform to extend Quinn’s work to continuous pitch and pitch-class sets, demonstrate distance measures in continuous Fourier spaces that correlate strongly with existing interval-based similarity measures, and gives a sample of how these continuous spaces can be used to investigate the structural properties underlying the Z-relation (the latter based on joint work with Rachel Hall).
Continuous harmonic spaces, Journal of Music Theory 51.2, 2007 (published in 2009). Winner of the David Kraehenbuehl Prize.
Generalized Voice-Leading Spaces
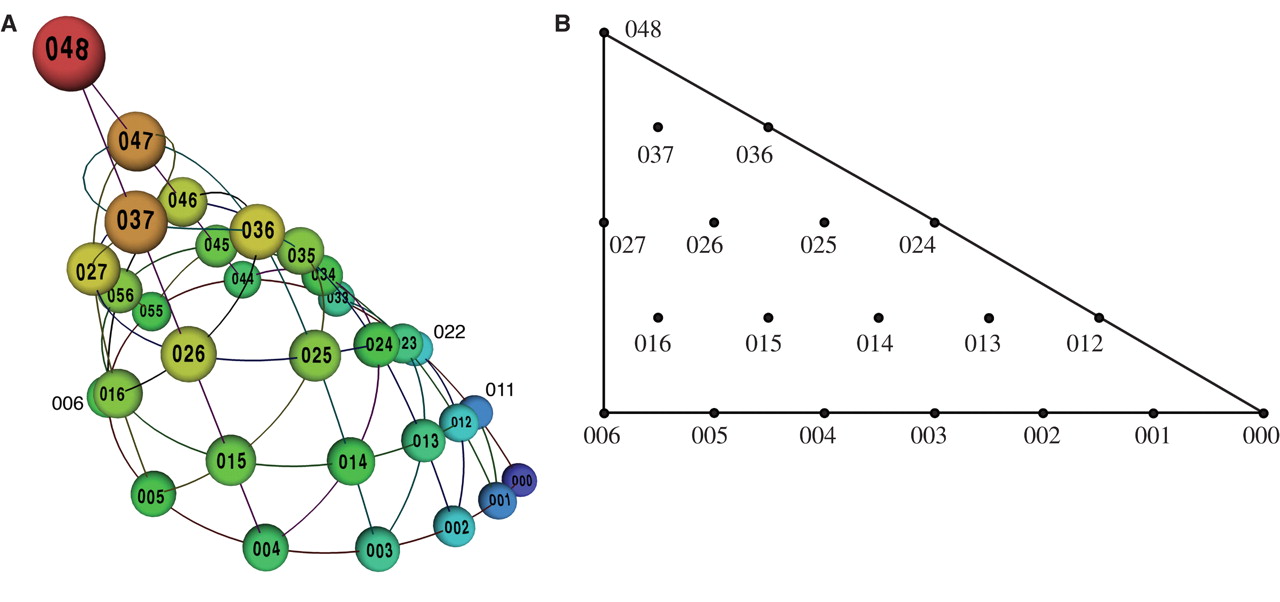
This is a three-way collaboration with Ian Quinn and Dmitri Tymoczko that, in the process of developing a very general geometric model of voice leading, recasts much of contemporary music theory in terms of a continuous, geometrical approach that contrasts with the discrete, combinatorial approach dominant in the field. The key is to form mathematical quotient spaces where points correspond to classes of chords and paths between points correespond to classes of voice leadings. There’s also lots of cool pictures, so have a look!
Callender, Clifton, Ian Quinn, and Dmitri Tymoczko. Generalized Voice-Leading Spaces. Science 18 April 2008: Vol. 320 no. 5874. Detailed supplemental material.
Lamento Motif and Jazz Harmonies in György Ligeti's Arc-en-ciel

This analysis focuses on the voice-leading and harmonic constraints underlying many of the chord progressions in Ligeti’s fifth Piano Etude, which the composers describes as “almost a jazz piece.” Ligeti’s harmonic approach in this etude seems less systmatic than many of his other works, but extending Neo-Riemannian approaches to efficient motions between tertian harmonies of indefinite size reveals the basic principles at work and the multiple laments implicit in the texture.
Interactions of the lamento motif and jazz harmonies in György Ligeti’s Arc-en-ciel. Intégral 2007.
Continuous Transformations
The point of departure for this paper is Kaija Saariaho’s Vers le blanc, the pitch structure of which consists of a continuous glissando between two chords over a duration of 15 minutes. About this work the composer writes, “The harmony is a continuous stream and cannot be heard as a series of changing chords. One only notices from time to time that the harmonic situation has changed.” What are these harmonic ‘situations’?
The solution offered in this paper is to consider this and other continuous transformations as trajectories through continuous spaces of chords, rhythms, tempos, etc. While the paper focuses on a number of specific examples, the theoretical ideas build on work by John Roeder (1987) and lay the groundwork for the later Science article on “Generalized Voice-Leading Spaces.”
Continuous Transformations, Music Theory Online 10.3, 2004.
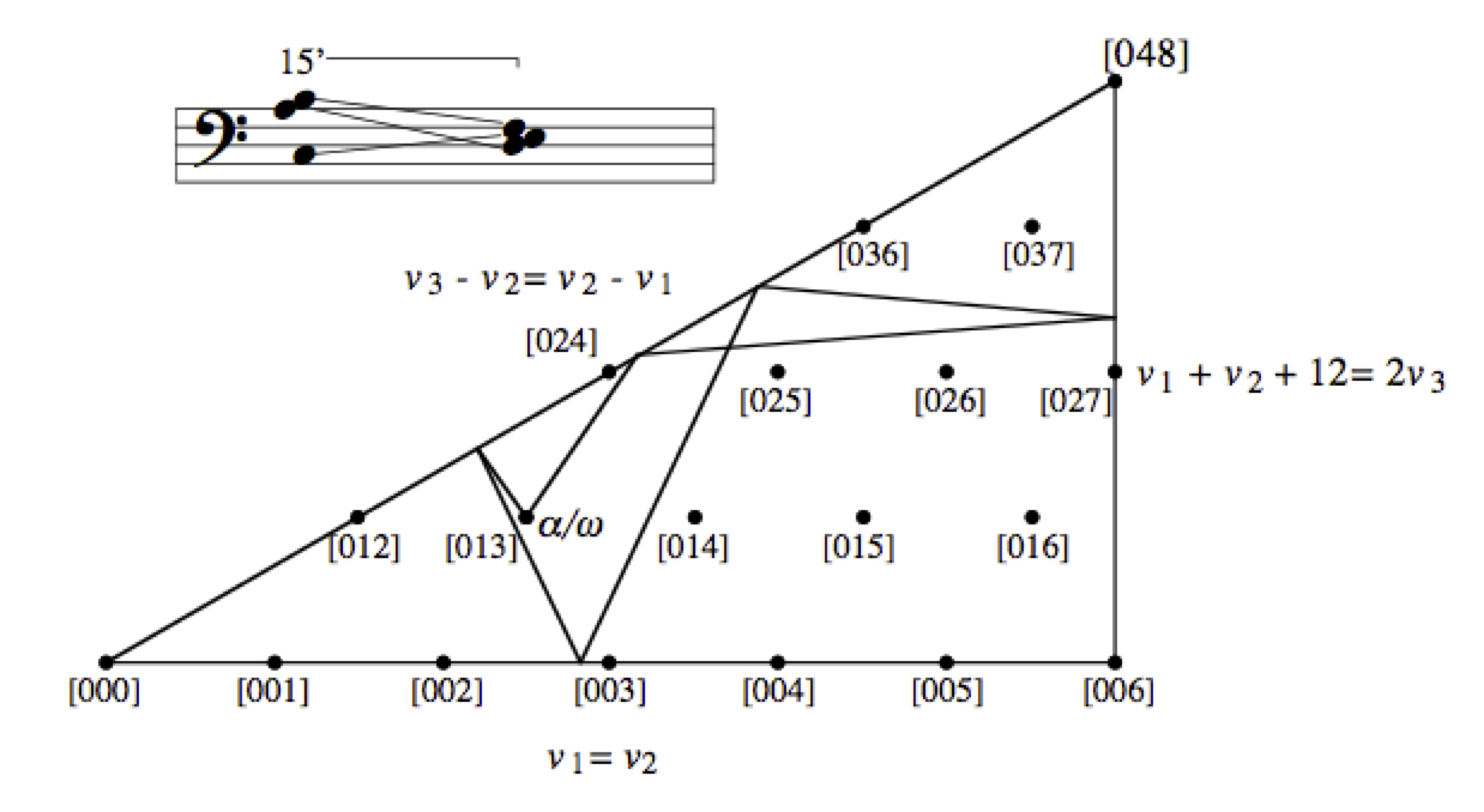
Formalized Accelerando
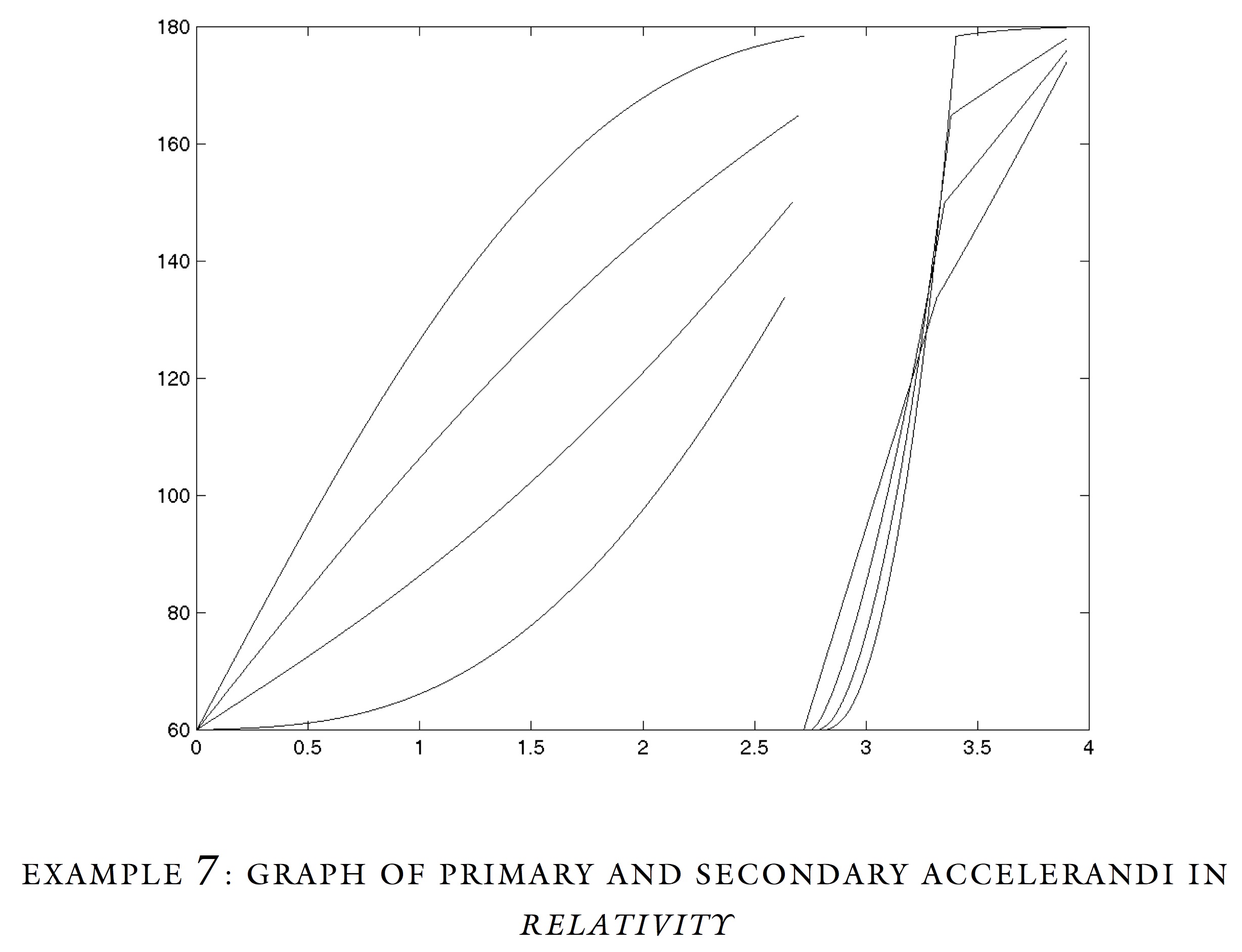
Of his fifty-one Studies for player piano, Nancarrow wrote only three canons based on large-scale continuous acceleration: Studies 21, 22, and 27. About these canons Kyle Gann writes, “[A]cceleration canon does not have the kind of clean structural implications Nancarrow found in the straight tempo canon … Perceptually fascinating, it did not lead to the kind of compositional richness he found elsewhere.”
The purpose of this paper is to explore the nature of Nancarrow’s conception of accelerando, and the manner in which his approach to acceleration canons limited the structural elements which proved so useful in the straight tempo canons. Having identified the problems with this approach, I consider a generalized model of acceleration, borrowing from calculus. The latter portion of the paper considers examples which exploit the potentials of this more general approach.
Formalized Accelerando, Perspectives of New Music 39.1, 2001.
Voice-Leading Parsimony in Scriabin
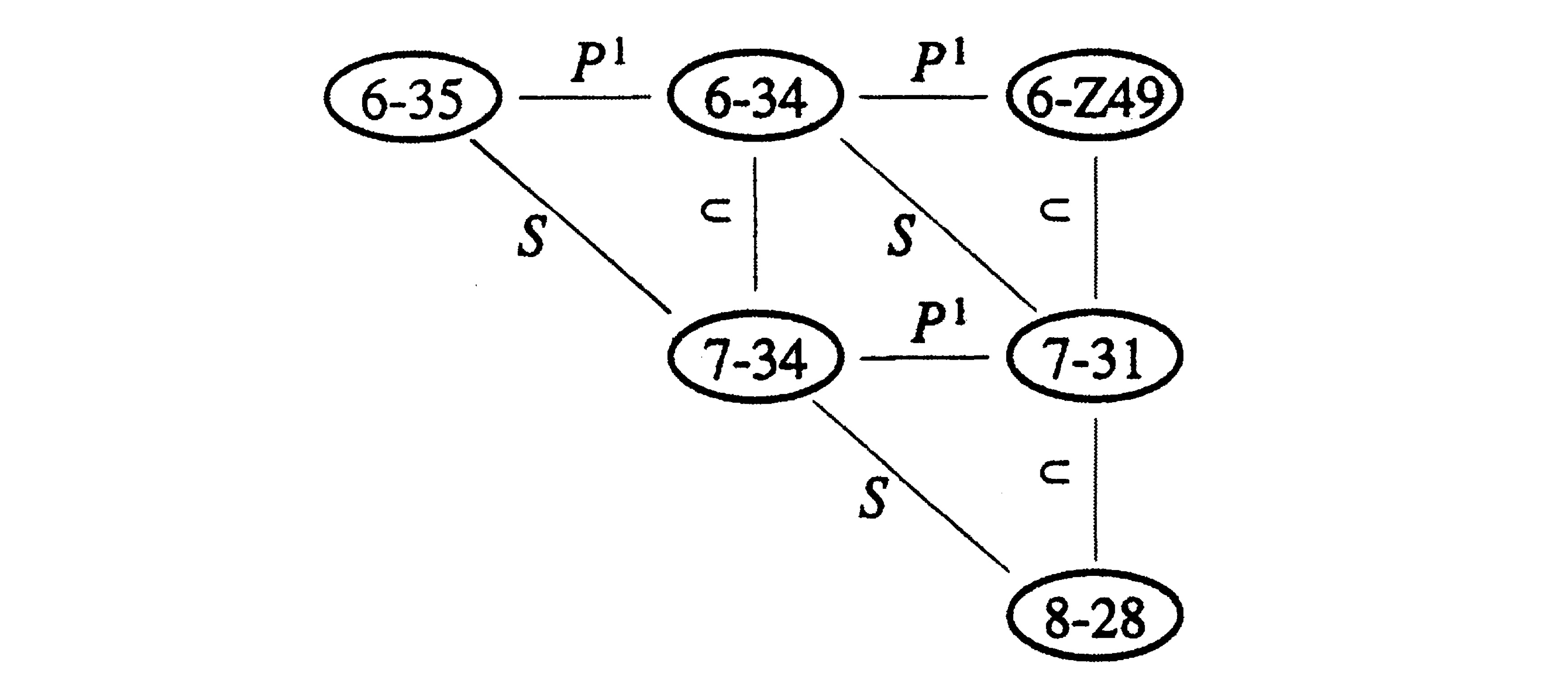
This paper is an extension of neo-Riemannian theory to the most prominent collections in Scriabin’s late work, which include the whole-tone, mystic, acoustic, and octatonic (as well as ♭2 variants of the mystic and acoustic), motivated by analysis of the third of the Three Etudes, op. 65. These collections are all related by minimal (or parsimonious) alterations, including displacing a single pitch class (pc) by semitone, adding or removing a single pc, and splitting a single pc into its chromatic neighbors (or the fusing of a whole tone into a single pc). The resulting relational network highlights the acoustic collection as an important mediating sonority between whole-tone and octatonic collections.
Voice-Leading Parsimony in the Music of Alexander Scriabin, Journal of Music Theory 42.2, 1998.